Fluid Mechanics and Machines & Hydrology PYQ – TN TRB Lecturer
11. Water flows upward through a vertical pipe of diameter 5 cm and height 10 m. For a constant discharge, the pressure head at the lower end of the pipe is 20.4 m. If there is no loss, the pressure head at the upper end of the pipe is _____ .
[TN TRB 2012: 2 Marks]
- 10.4 m
- 104 m
- 1.04 m
- 101 m
Explanation:
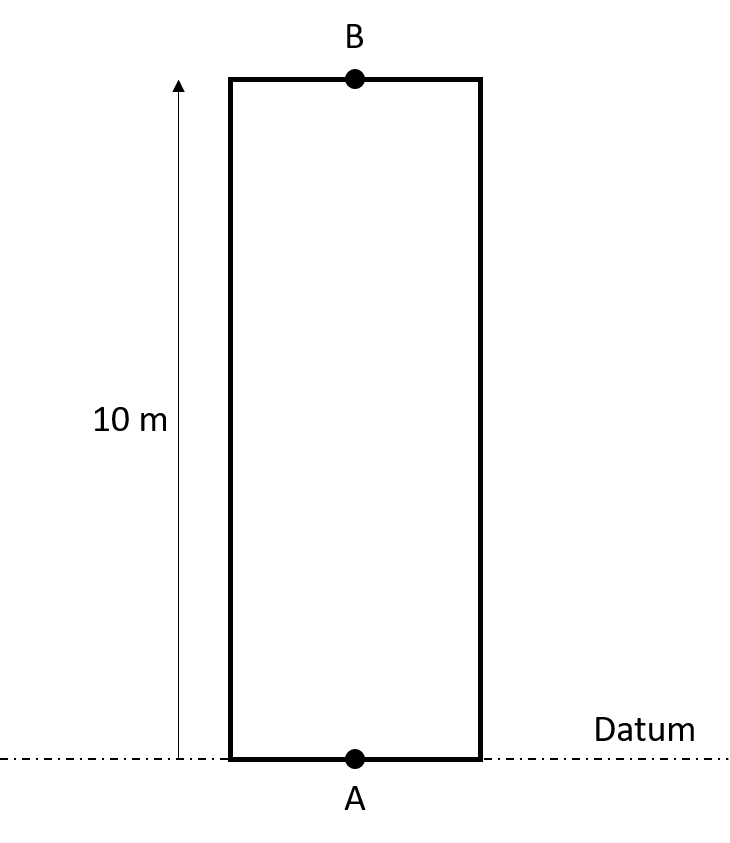
Consider the lower end of pipe (point A) as datum.
Here,
ρg
= 20.4 m, hL = 0,
ZA = 0, ZB = 10.0 m
As the discharge and cross-section are constant, VA = VB = V
Applying Bernoulli’s equation at points A and B,
ρg
+
2g
+ ZA
=
ρg
+
2g
+ ZB + hL
⇒ 20.4 +
2g
+ 0 =
ρg
+
2g
+ 10 + 0
⇒ 20.4 =
ρg
+ 10
⇒
ρg
= 10.4 m
Hence, the pressure head at top end of pipe = 10.4 m
12. Modal analysis of free surface flows are based on _____ .
[TN TRB 2012: 2 Marks]
- Reynolds number
- Froude number
- Mach number
- Euler number
Explanation:
Froude’s model law is used,
- In the design of spillways, weirs.
- To analyze free surface flow like open channels, rivers, etc.,
- To analyze the flow of jet from an orifice or a nozzle.
13. The specific speed of a turbine is given by _____ .
[TN TRB 2012: 2 Marks]
NS =
N√ P H3/4NS =
N√ Q H3/4NS =
N √ P H5/4NS =
NP5/4 √ H
Explanation:
Specific speed of a turbine is the speed of a symmetrical turbine of such size that it will develop unit power when operated under unit head.
The formula to calculate the specific speed of turbine (NS) is,
NS =
H5/4
14. The condition satisfied by the three routing coefficients of the Muskingum method is _____ .
[TN TRB 2012: 2 Marks]
- C0 + C1 + C2 = 1
- C0 + C1 + C2 = 0
- C0/C1 = C1/C2
- C0 C1 C2 = 1
Explanation:
The condition satisfied by Muskingum method’s routing coefficients is,
Where,
C0 =
K(1 – x) + 0.5Δt
C1 =
K(1 – x) + 0.5Δt
C2 =
K(1 – x) + 0.5Δt
15. Blaney – Criddle method is used to determine _____ .
[TN TRB 2017: 1 Mark]
- Evaporation
- Consumptive use of crop
- Infiltration
- Interception
Explanation:
Methods of measurement of consumptive use (or) evapo-transpiration of crop:
- Penman’s equation
- Blaney Criddle’s formula
- Using Lysimeter
- Using Field plots
16. Storage capacity of a reservoir can be fixed by _____ .
[TN TRB 2017: 1 Mark]
- Mass curve method
- Storage zones method
- Dicken’s formula
- Ryve’s formula
Explanation:
Storage capacity of a reservoir can be determined by using mass curve technique.
17. Crop period is the time a crop takes _____ .
[TN TRB 2017: 1 Mark]
- First time of watering to last watering
- From sowing to its harvesting
- From sowing to last watering
- From first watering at the time of sowing to its harvesting
Explanation:
Crop period is the time interval between the instant of sowing of seed and the instant of harvesting of the crop. It is the total time during which the crop is present in the field.
18. If pipes of different lengths and diameters are connected with one another to form a pipeline, such a pipeline is called _____ . If such a pipeline is replaced by a single pipe of same diameter with the same rate of flow, loss of head and length is called ______ .
[TN TRB 2017: 1 Mark]
- Compound pipe and Pipe in series
- Compound pipe and Equivalent pipe
- Pipes in series and Compound pipe
- Pipes in series and Uniform pipe
Explanation:
- Pipes of different length and diameter connected in series or parallel are called compound pipe.
- An equivalent pipe is a pipe of uniform diameter having the same head loss and same rate of flow of a compound pipe.
19. Specific speed of a turbine can be calculated using the formula _____ .
[TN TRB 2017: 1 Mark]
NS =
πDN 60NS =
N√ P H3/4NS =
πDNT 4500NS =
N√ P H5/4
Explanation:
Specific speed of a turbine is the speed of a symmetrical turbine of such size that it will develop unit power when operated under unit head.
The formula to calculate the specific speed of turbine (NS) is,
NS =
H5/4
20. The critical specific energy for a flow of 12 m3/s in a rectangular channel of width 3.5 m and energy coefficient 1.1 will be _____ .
[TN TRB 2017: 1 Mark]
- 3.127 m
- 1.645 m
- 1.345 m
- 1.096 m
Explanation:
Discharge per unit width, q =
B
=
3.5
= 3.43 m3/s per m channel width
Critical depth, yc = {
g
}1/3 = {
9.81
}1/3 = 1.06 m
Velocity, V =
Ac
=
3.5 x 1.06
= 3.23 m/s
Thus, Critical Specific Energy, Ec = yc +
2g
⇒ Ec = 1.06 +
2 x 9.81
⇒ Ec = 1.645

